Abstract
What did i do?
I've measured my resting heart rate circadian rhythm, to check the diurnal difference of day and night.
How did i do it?
I've used Fitbit Charge 4 placed on wrist to measure HR.
What did i learn?
My resting HR diurnal changes looks strong and Fitbit Charge 4 was able to detect them. The difference of day and night is 19 beats per minute with large effect size.
Introduction
Circadian rhythm disorders may decrease our healthspan and increase occurrence chronic diseases during aging. Having same resting HR at day and night may indicate a health issues.
The purpose of this experiment (n=1) is to find diurnal changes in resting HR.
Materials & Methods
Participants
Adult male (n=1) anthropometrics was described in previous article
Experimental design
From 2021-06-01 to 2021-06-28 (28 days) heart rate was measured by Fitbit Charge 4 placed on wrist 1cm away from bone and wearing it tight enough to have good contact with skin. Fitbit heart rate and steps was exported in 1 minute resolution. Resting HR (RHR) was defined as HR measurement with zero steps for 10 preceding minutes.
Results
Visual inspection of data reveals large diurnal changes and looks similar to body temperature rhythm:
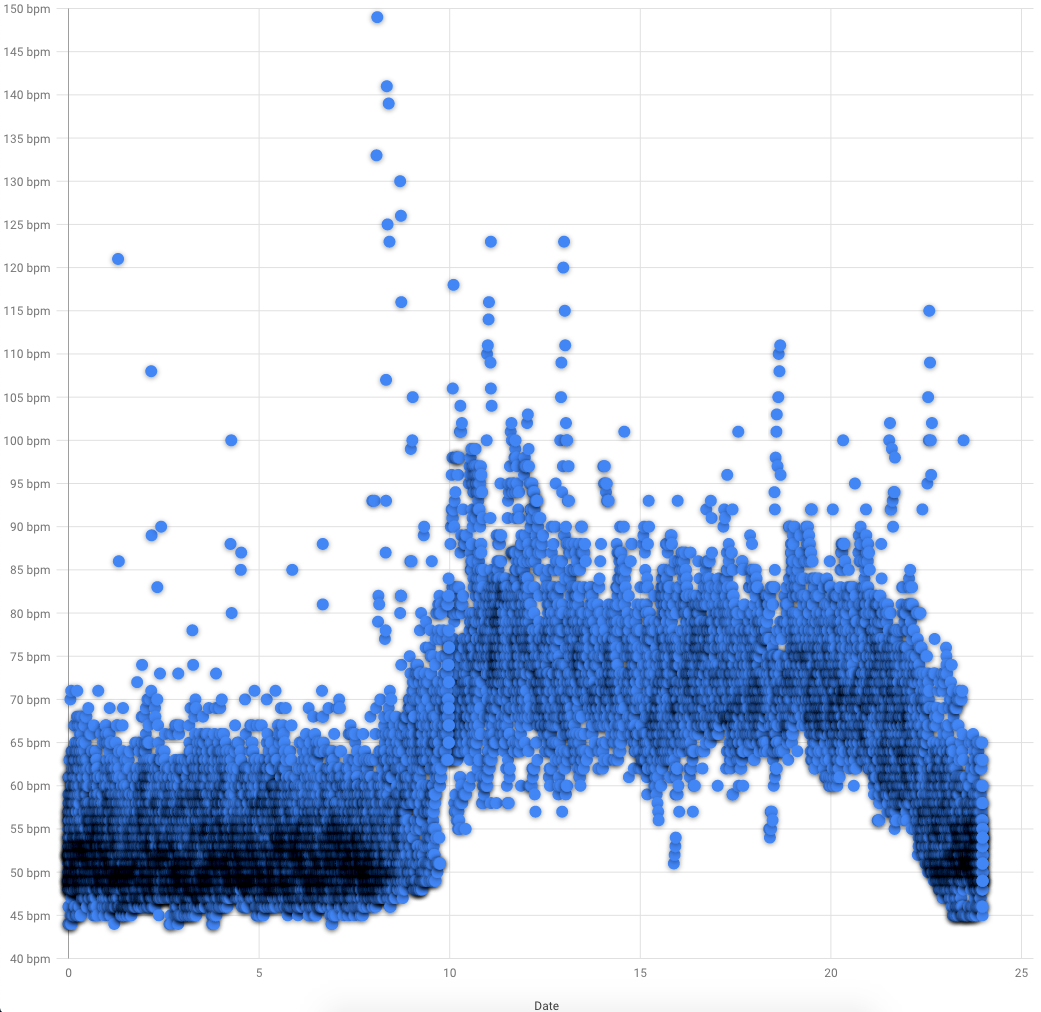
Blue dots is a resting HR in bpm. X axis is a hour of day. Google Developer charts for some reasons doesnt show decimal point for temperature and adding empty 25 hour. Measurements density highlighted by shadowing.
We can see some outliers, but i didnt removed them because of a large sample size (n ~ 20 000)
Day vs Night RHR, bpm
| Mean | 95% CI | |
| Day (9:00 - 19:00) | 73.01 | [72.76, 73.25] |
| Night (21:00 - 7:00) | 54.04 | [53.94, 54.15] |
Confidence intervals for means a pretty narrow and far away enough to prove statistically significant difference between day and night.
Group differences
| Effect size | 95% CI | |
| Hedges g | Large | [-2.653, -2.653] |
| Mean difference, bpm | -18.95 | [-18.95, -18.95] |
We can see a extremely narrow CI's showing a difference of 19bpm between day and night with "Large" effect size.
Discussion
The main result of that experiment is 19bpm difference between day and night which acts as a proxy of my circadian rhythm. I'll continue checking it in future, to see the trends.
Measuring RHR with Fitbit Charge 4 is convenient enough to be used in long term for monitoring diurnal changes.
Data availability & Information
Welcome for questions, suggestions and critics in comments below.
Data is fully available here.
library(goftest)
library(dplyr)
library(effectsize)
library(lubridate)
library(ggplot2)
library(boot)
fitbit <- read.csv("https://blog.kto.to/uploads/circadian-rhr-fitbit.csv")
fitbit <- fitbit[!is.na(fitbit$RHR),]
#filter 21:00 - 7:00 as group 1, 9:00 - 19:00 as group 2, other as group 0
fitbit <- fitbit %>% select(datetime,RHR) %>%
mutate(group = if_else(((hour(datetime) >= 21) | (hour(datetime) <= 7)), 1,
if_else(((hour(datetime) <= 19) & (hour(datetime) >= 9)),2, 0)));
#remove group 0
fitbit <- fitbit[fitbit$group != 0,]
#check for normality distribution
st <- ad.test(fitbit$RHR) #shapiro.test for n < 5000, ad.test othervise
if_else(st$p.value < 0.05, 'non-uniform distribution', 'uniform distribution')
bootMean <- function(data, i) { d <- data[i]; return(mean(d)); }
bootMeanDiff <- function(data, i)
{
d <- data;
data_group1 <- !is.na(d$group)&d$group == 1
data_group2 <- !is.na(d$group)&d$group == 2
g1 <- d$RHR[data_group1]
g2 <- d$RHR[data_group2]
return(mean(g1) - mean(g2));
}
bootHedgesG <- function(data, i) #calc hedges G to measure effect sizes
{
d <- data;
data_group1 <- !is.na(d$group)&d$group == 1
data_group2 <- !is.na(d$group)&d$group == 2
g1 <- d$RHR[data_group1]
g2 <- d$RHR[data_group2]
h <- hedges_g(g1, g2)
return(h$Hedges_g[1]);
}
#bootstrap hedges G effect size between group 1 and 2
results <- boot(data=fitbit, statistic=bootHedgesG, R=10000)
boot_result <- boot.ci(results, type = c("perc")); boot_result;
interpret_g(-2.653, "cohen1988");
#bootstrap mean difference between group 1 and 2
results <- boot(data=fitbit, statistic=bootMeanDiff, R=10000)
boot_result <- boot.ci(results, type = c("perc")); boot_result;
interpret_g(-2.653, "cohen1988");
#take out group 1 and 2 from dataset
data_group <- !is.na(fitbit$group)&fitbit$group == 1
day <- fitbit$RHR[data_group]
data_group <- !is.na(fitbit$group)&fitbit$group == 2
night <- fitbit$RHR[data_group]
#calc averages & CI
results <- boot(data=day, statistic=bootMean, R=10000)
day_result <- boot.ci(results, type = c("perc")); day_result;
results <- boot(data=night, statistic=bootMean, R=10000)
night_result <- boot.ci(results, type = c("perc")); night_result;
[1] "non-uniform distribution"
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 10000 bootstrap replicates
CALL :
boot.ci(boot.out = results, type = c("perc"))
Intervals :
Level Percentile
95% (-2.653, -2.653 )
Calculations and Intervals on Original Scale
[1] "large"
(Rules: cohen1988)
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 10000 bootstrap replicates
CALL :
boot.ci(boot.out = results, type = c("perc"))
Intervals :
Level Percentile
95% (-2.653, -2.653 )
Calculations and Intervals on Original Scale
[1] "large"
(Rules: cohen1988)
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 10000 bootstrap replicates
CALL :
boot.ci(boot.out = results, type = c("perc"))
Intervals :
Level Percentile
95% (-18.95, -18.95 )
Calculations and Intervals on Original Scale
Intervals :
Level Percentile
95% (-0.4946, -0.4563 )
Calculations and Intervals on Original Scale
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 10000 bootstrap replicates
CALL :
boot.ci(boot.out = results, type = c("perc"))
Intervals :
Level Percentile
95% (53.94, 54.15 )
Calculations and Intervals on Original Scale
BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
Based on 10000 bootstrap replicates
CALL :
boot.ci(boot.out = results, type = c("perc"))
Intervals :
Level Percentile
95% (72.76, 73.23 )
Calculations and Intervals on Original ScaleStatistical analysis
RStudio version 1.3.959 and R version 4.0.2. Confidence Intervals was build using bootstrap percentile. Effect sizes based on Hedge's g, Cohen's 1988 rules