Introduction

In my previous analysis [1] [2] of caffeine versus sleep i've used classical frequentists approach to model caffeine - sleep relationship. Here i'm going to use Bayesian data analysis and better sleep data derived from multichannel EEG.

Bayesian approach will offer a posterior distribution which can be used to calculate expected value / loss for making a decision.

Methods

During each night a multichannel EEG were recorded to sd card by using OpenBCI Cyton with 500Hz sampling rate, Gold cup electrodes + Ten20 paste placed on Frontal, Temporal and Occipital regions. YASA were used to score hypnograms for each channel and then consensus hypnogram were built. Total sleep time, TST = N3 + N2 + N1 + REM were used as outcome parameter.

Caffeine intake for each day were recorded and days were split into 2 groups: days with caffeinated coffee (caff) and with decaffeinated (decaff) by "swiss water" method. Both groups were split into 2 subgroups: weekend and weekdays. I drink standard portion of coffee once a day in the morning on for simplicity i will be grouping days and doing BEST for groups.

In a total 4 groups were analysed: caff-weekday, caff-weekend, decaff-weekday and decaff-weekend.

Data analysis

Bayesian data modeling starts from describing parameters of interest and their priors.

TST is a time, which always take positive values and healthy sleep is around 5 sleep cycles * 90 minutes each, totally ~450 minutes. What's the easiest distribution to start with for that find of data? If you ask ChatGPT the answer will be a Poisson. For sure there might be a better distributions where we can control variation, but Poisson is a simple one. Here is how data looks like against Poisson with lambda=450

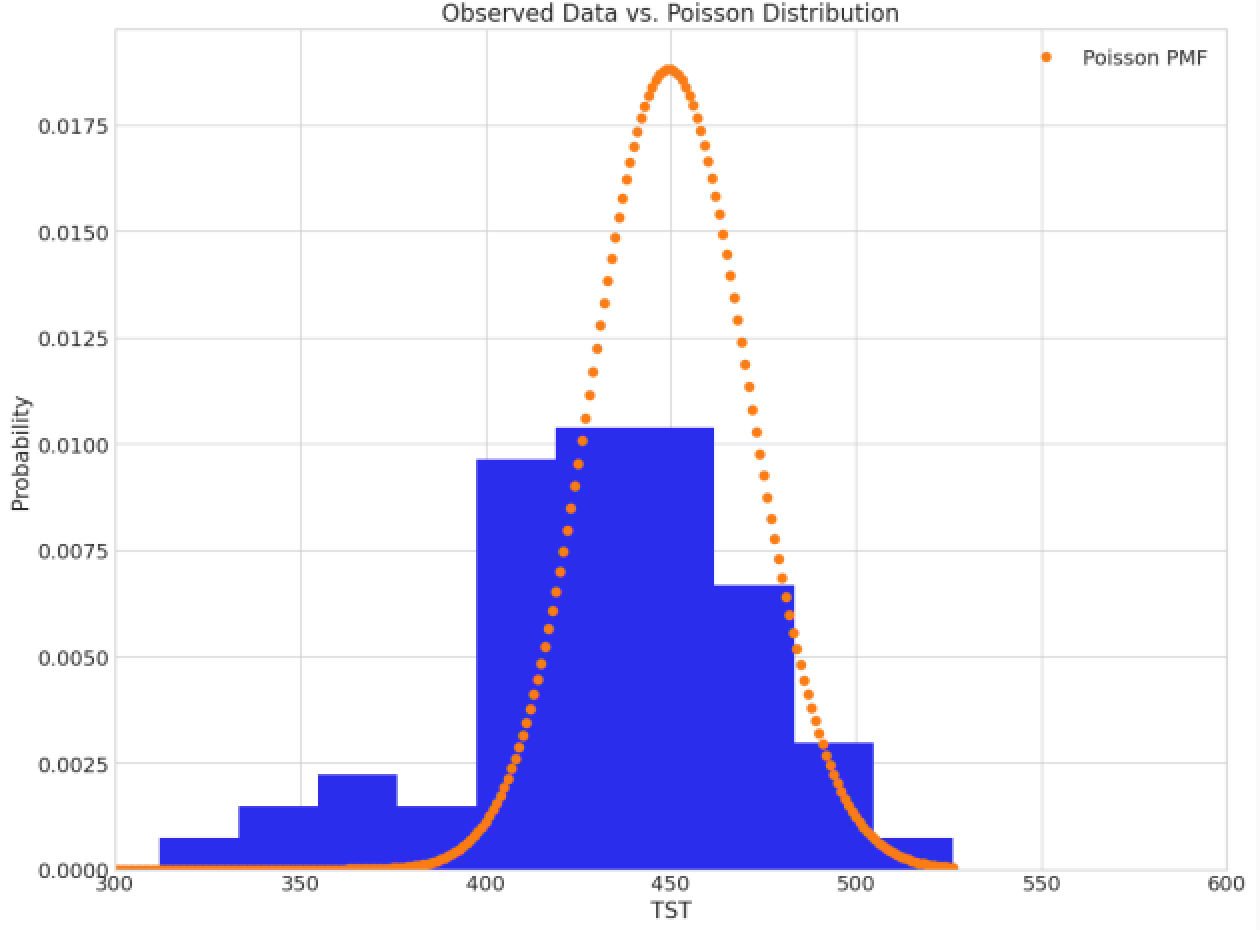
This doesnt fit well, but for a prior we are not looking for best fit, it should generally catch our prior knowledge: TST is positive number, concentrated around 450. This will be a hyperprior which will serve as a population prior. Group priors will be Poisson with lambda drawn from hyperprior and will be passed into likelihood.

This simple model will look like that:

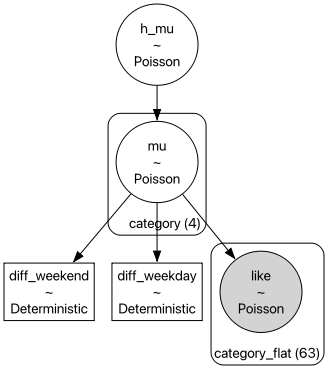
"h_mu" is a population hyperprior, "mu" is group level prior (4 groups) and "like" is a likelihood function into which we will pass data (n=63)

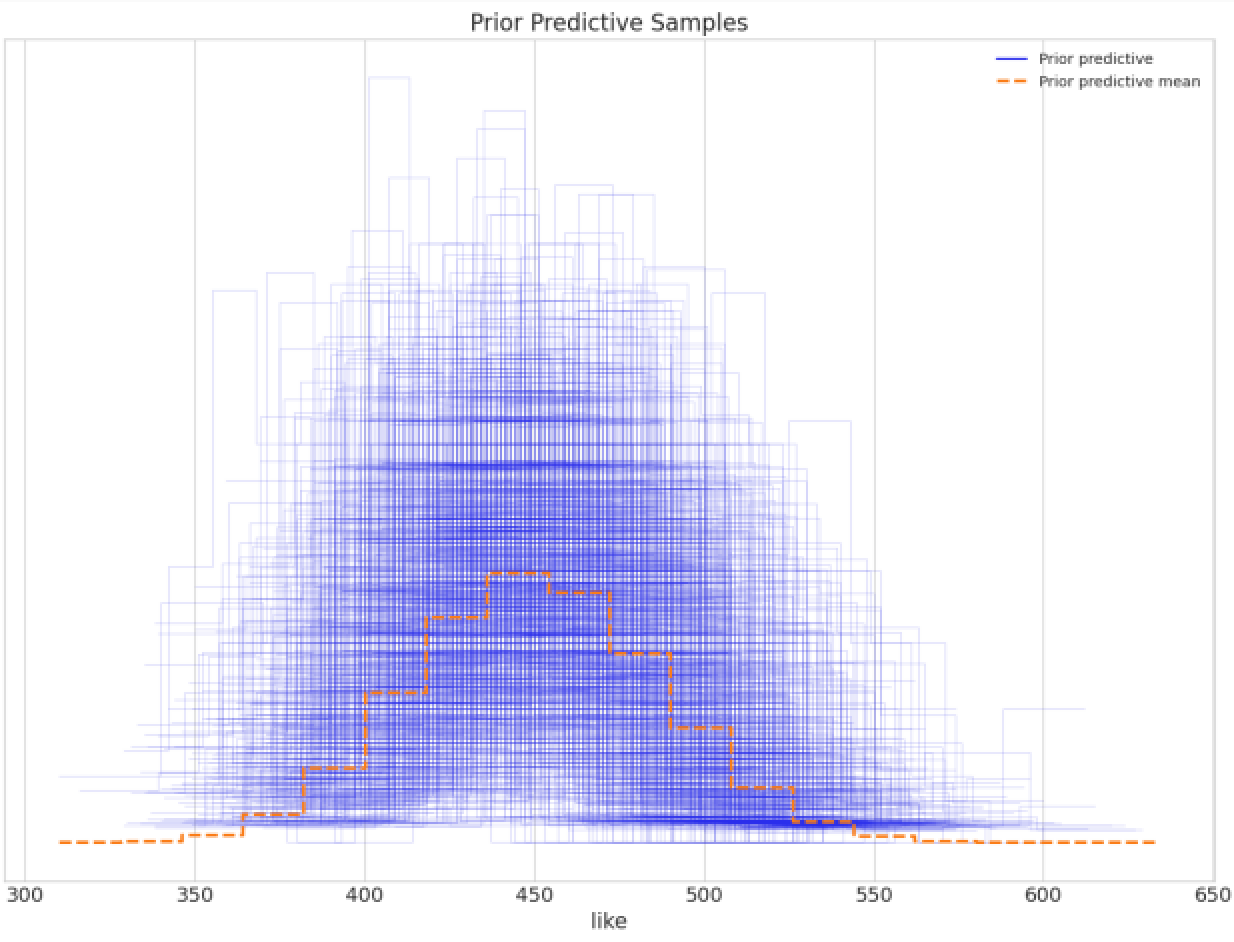
Prior predictive check seems to be hairy and this is expected for not so big dataset. Prior predictive mean seems to be somewhere near 450.

Lets look at trace to see how our sampling from posterior gone:

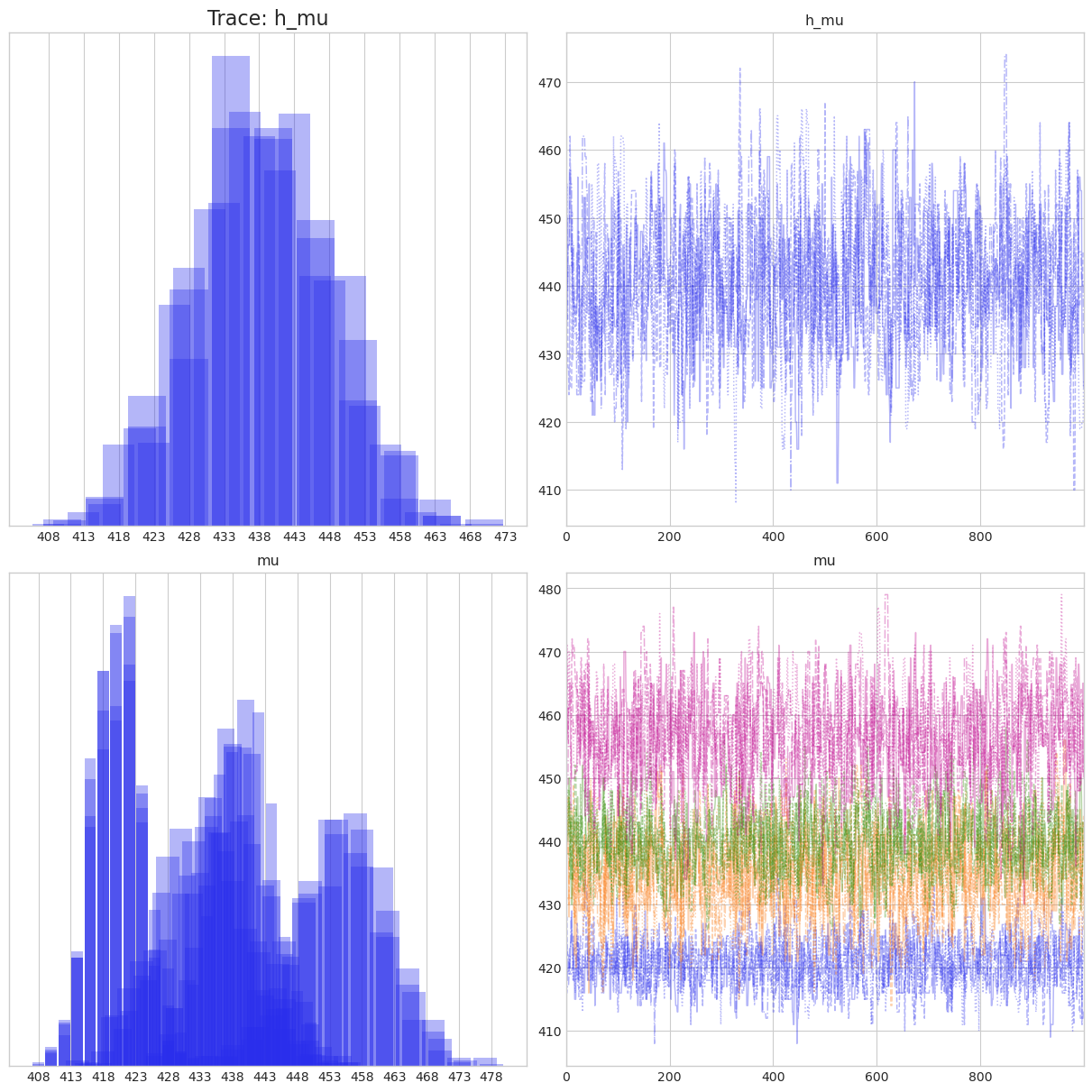
Traces on the right looks good enough. Also for mu, which is a group level priors we can see 3 distinct groups (not colored for some reason, but can be clearly seen from right plot). Hyperprior h_mu is around 438 minutes.

Here is short summary for our groups, differences can be clearly seen:

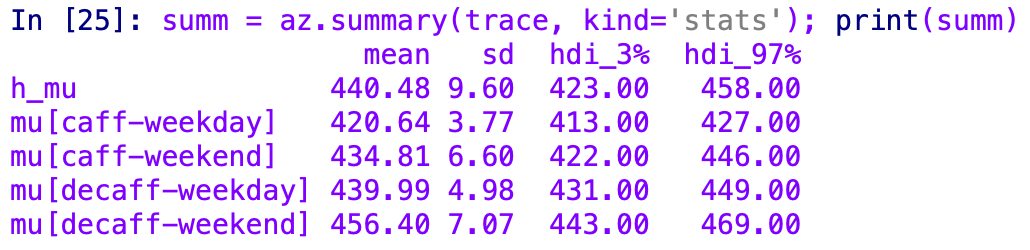
Lets plot posterior distributions:

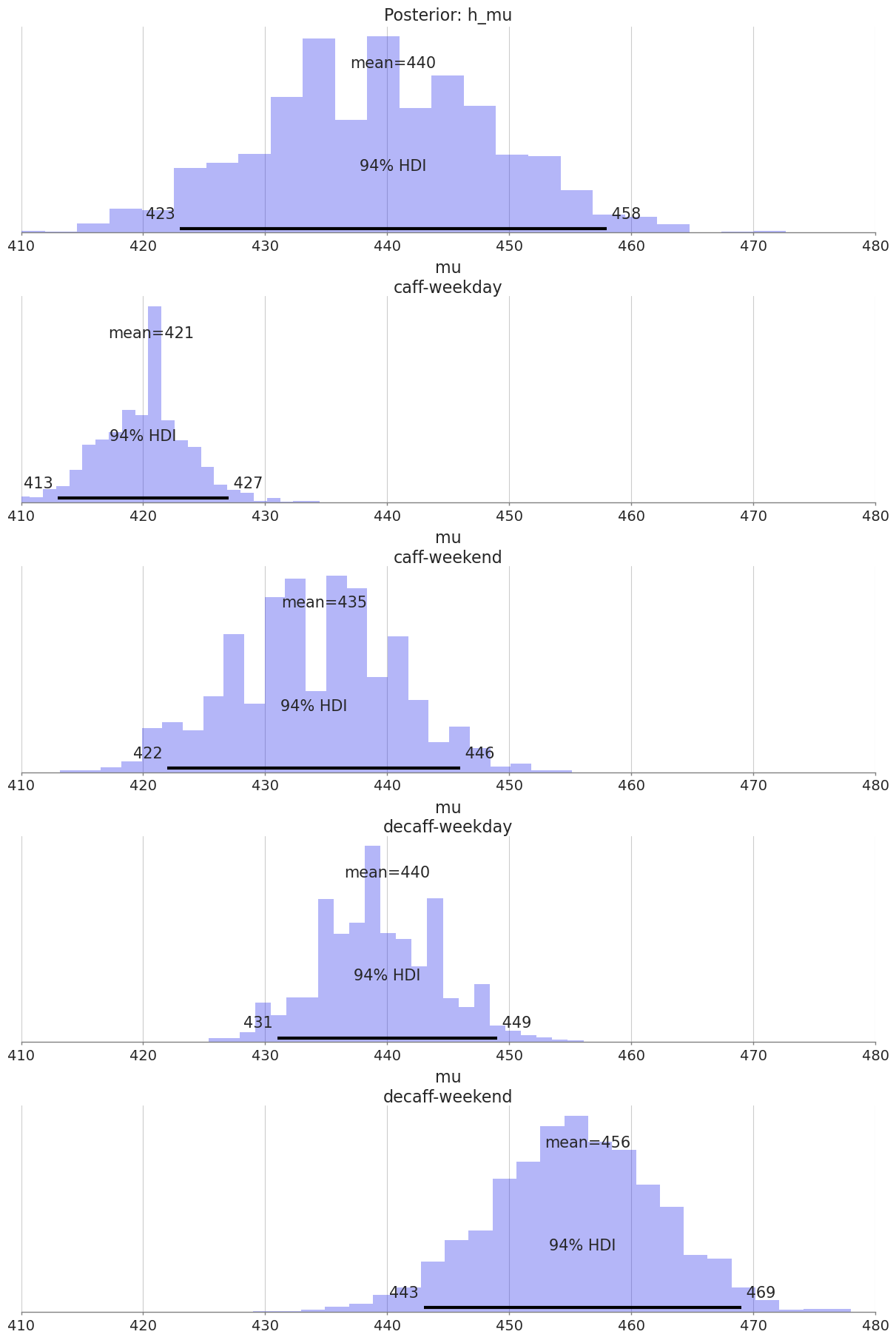
94% HDI stands for High Density Interval - interval where 94% of probability density is concentrated. Also we can see group means.

Lets look how prior h_mu changed after we pass some data:

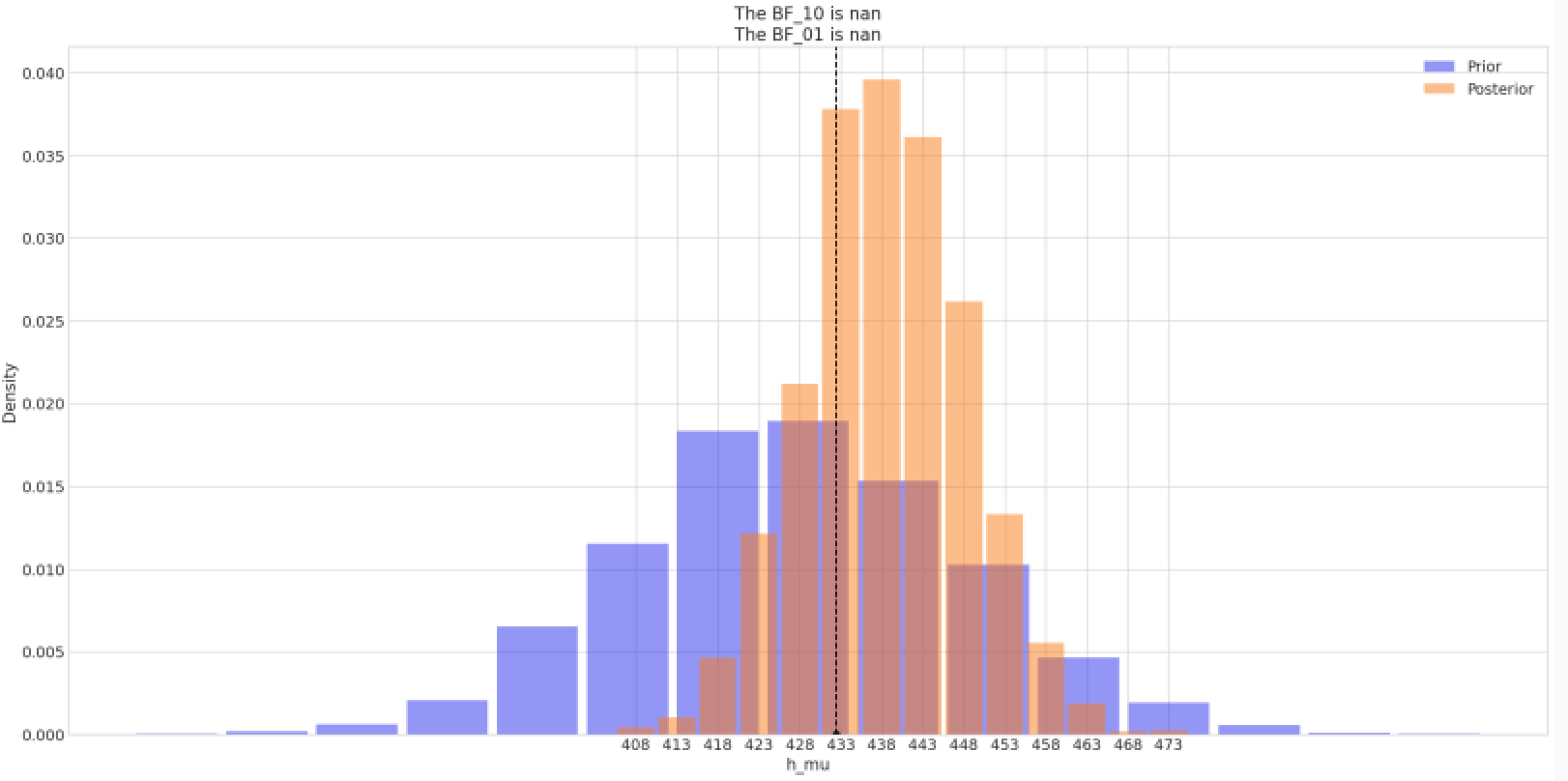
Here we can see that from wide less informative prior it shifted to more concentrated posterior, as expected.

Lets do posterior predictive checks to see how our posterior distribution fits data:

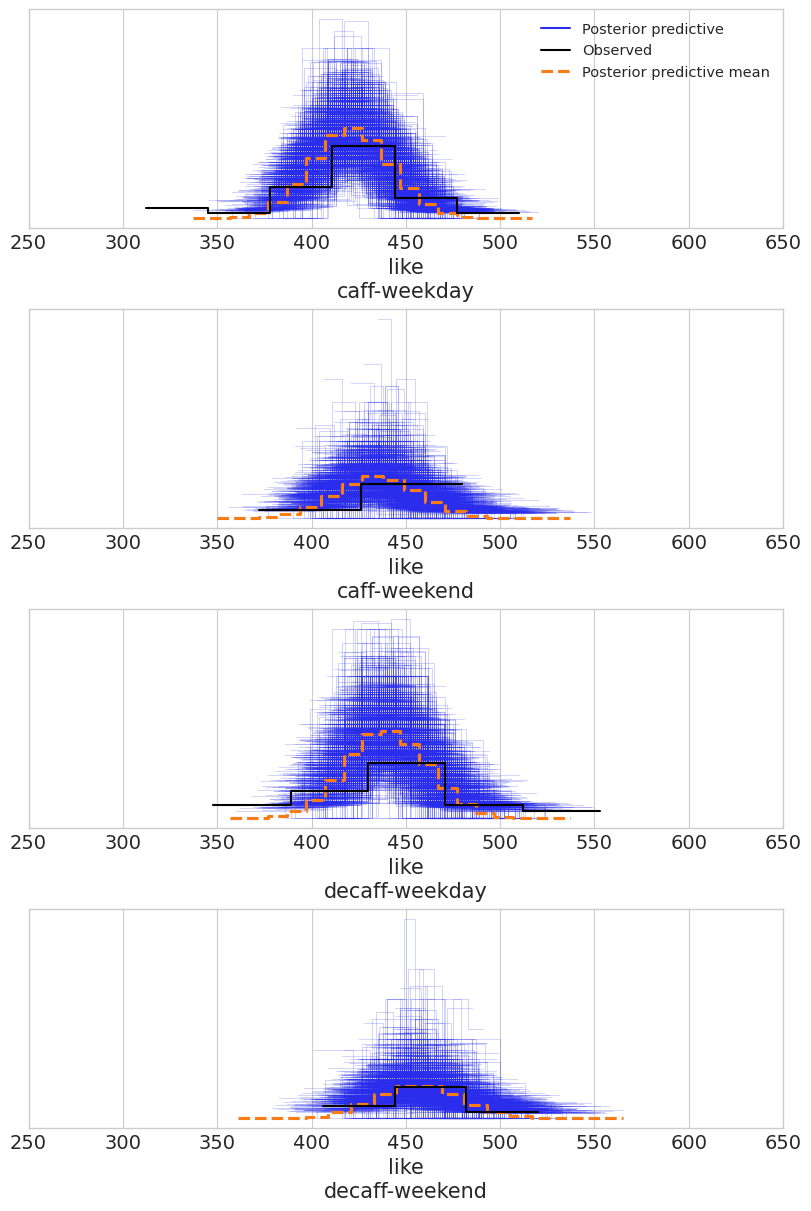
It seem to be hairy as for prior, but black line (observed data) somehow agree with posterior predictive mean.

Lets get to the final stage and look for difference between groups:

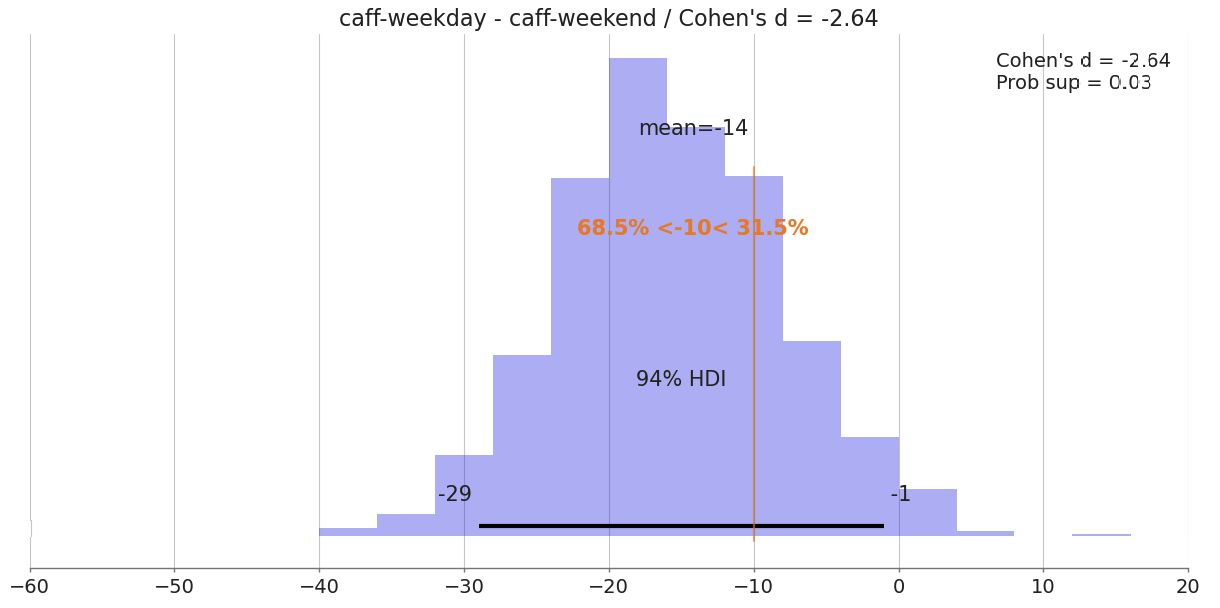
Here we can see that during caff days there is difference in TST for weekday vs weekend with mean -14 minutes. The probability is 68% for effect being at least -10 minutes. Not a huge one but we can see a direction and there is 97% probability that effect is less then zero (negative).

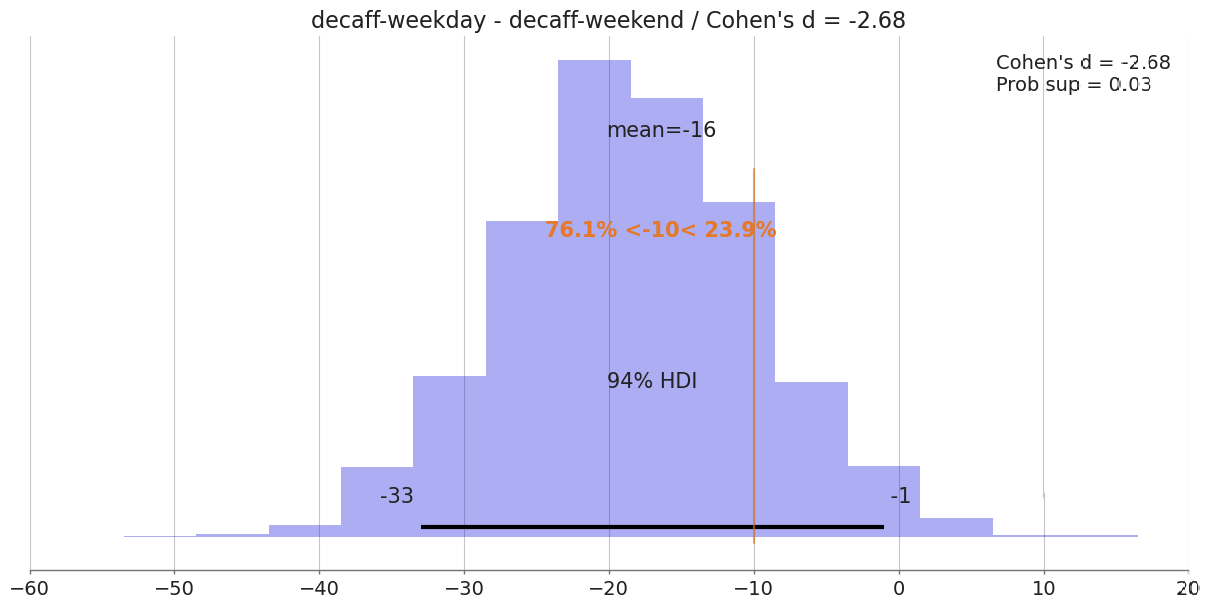
Interestingly same happens for decaff days. 76% probability that there is at least 10 minutes less sleep during weekdays. So independently to caffeine, during weekdays (when i work mostly) I sleep less. 

Lets look what caffeine do to my sleep:

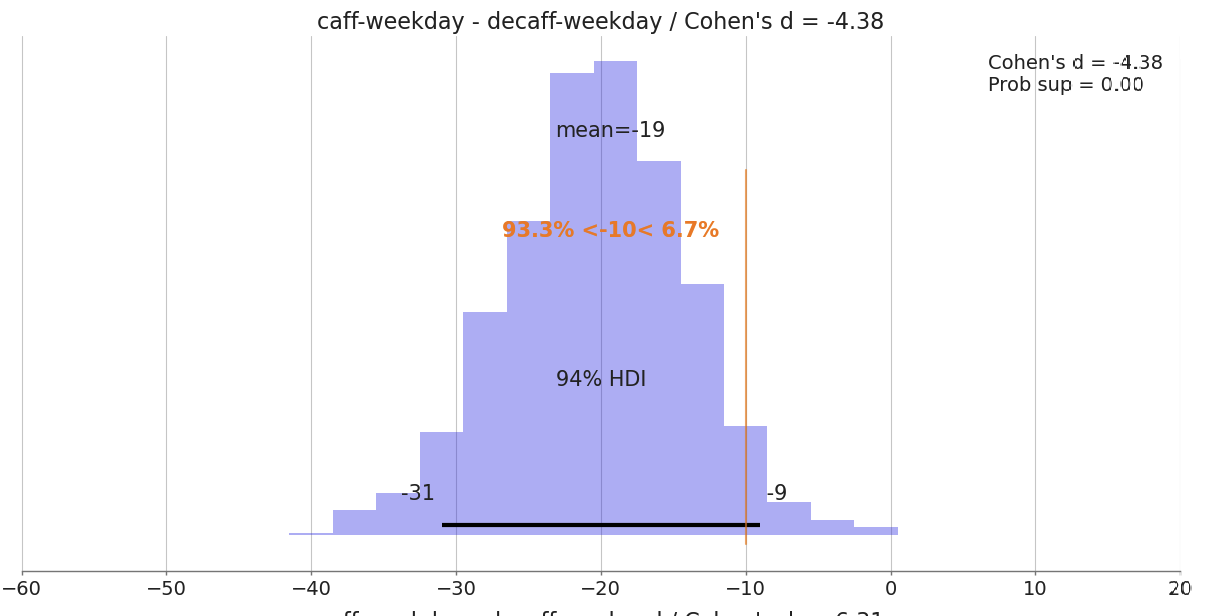
We can see that during weekdays caffeine results in -19 minutes of sleep on average and with 93% probability effect is at least -10 minutes.

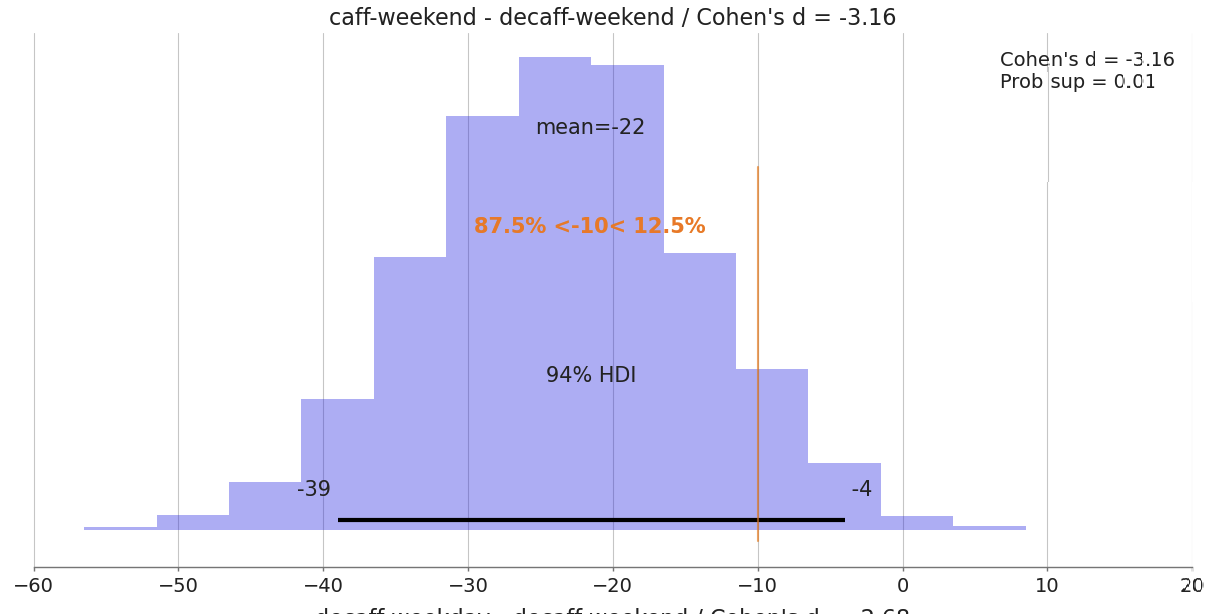
Same stand for weekends. During weekend i lose 22 minutes of sleep on average due to caffeine. 88% probability effect is at least -10 minutes.

So from here i can conclude that weekdays and caffeine independently affect my sleep. If we go back to group means we can see that decaf weekend mean is 456 minutes and caff weekday mean is 421 minutes and thats a 35 minute difference due to both effects.

This post is a work in progress and i'm going to improve it soon. Code will be published on github.